Modern mathematical comments on Two Falling Globes

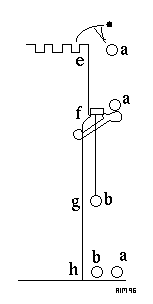
The experiment begins with the release of globe a at E. When a reaches the lever at F after time t₁, the string holding globe b is released: as a passes F, b begins to fall at G. The length of the string FG has been adjusted so that a and b land together at H. Let t₂ be the time taken for a to fall from F to H, and for b to fall from G to H.

First, let us analyse the problem assuming uniform acceleration, with value g. This corresponds to no air resistance. In this case, t, the time taken to fall a distance x is given by

t = sqrt ( 2 x / g ) [1]

For the Two Falling Globes experiment,

t₁ = sqrt ( 2 . EF / g ) [2]
t₂ = sqrt ( 2 . GH / g ) [3]
t₁ + t₂ = sqrt ( 2 . EH / g ) [4]

Substituting for t₁ and t₂ in [4] using [2] and [3], and cancelling sqrt ( 2 / g ), we get the elegant result that

sqrt ( EH ) = sqrt ( EF ) + sqrt ( GH ) [5]

By setting up this experiment and adjusting the length of the string FG so that a and b land together, equation [5] can be tested. Significant deviations from equality show that uniform acceleration is not happening for the distances and masses used (if the distances are too short or the masses too great, deviations from uniformity will be unmeasurable.)

In this way, one can demonstrate the presence of air resistance etc without a clock - very convenient for someone in Newton's position. However, it is not possible to determine g using this apparatus since in [2], [3] and [4] the times are all proportional to g^-½. None of the equations allow us to separate t from g^-½ since they are not linearly independent. In crude terms, we can choose any combination of t and g^-½ as long as the products are acceptable, eg that

t₁ g^½ = sqrt ( 2 EF )

Now take the case where the globes do not accelerate uniformly, but with acceleration given by

d²x / dt² = g - k . dx / dt [6]

so that the acceleration is reduced in proportion to the speed. Newton asserts the effect of air resistance takes this form (and we might assume that the reduced weight of moving bodies in his mechanical theory of gravity could too.) For air resistance, the constant k depends on the mass and size of the globes.

For a body falling from rest at time t=0, the solution of [6] is

x = ( g / k² ) . ( k t + exp ( - k t ) - 1 ) [7]

This can be verified by substituting into [6] (or by solving [6] by the change of variable v = dx / dt, to obtain v(t), and then integrating this.)

The uniform acceleration case with k=0 can be recovered by expanding the exponential as a series and cancelling. Only the term

(1/2) . g t² [8]

is independent of k and remains if k=0. This is equivalent to [1] above.

For the Two Falling Globes experiment with k not zero and two identical globes, t₁, t₂, k and g are linearly indepedent in the three equations giving EF, GH and EH in terms of t₁, t₂ and t₁ + t₂ based on [7]. However, we cannot solve a set of three equations for four unknowns.

Interestingly, Newton records an observation by Galileo which would provide a fourth equation and allows us to solve for the times and the two constants. This requires that the experiment is performed with a globe of the same size and mass as Galileo (so that k is the same.) Since Newton carefully notes the mass and material of the globe Galileo used, this would be possible. Newton's intentions are discussed on another page.