John Wallis
Born: 23 Nov 1616
in Ashford, Kent, England
Died: 28 Oct 1703
in Oxford, England

Click the picture above
to see four larger pictures
Show birthplace location
John Wallis went to school in Ashford, then moved to Tenterden where he first showed his great potential as a scholar. In 1630 he went to Felsted where he became proficient in Latin, Greek and Hebrew. From there he went to Emmanual College Cambridge where he first became interested in mathematics. Since nobody at Cambridge at this time could direct his mathematical studies, his main topic of study became divinity. He was ordained in 1640.
Wallis was skilled in cryptography and decoded Royalist messages for the Parliamentarians during the Civil War. It is suggested that he was appointed to the Savilian Chair of geometry at Oxford in 1649 because of this. Certainly the holder of the chair, Peter Turner, was dismissed for his Royalist views. Wallis held the chair for over 50 years until his death and, even if the reason for his appointment is true, he most certainly deserved to hold the chair.
Wallis was part of a group interested in natural and experimental science who started to meet in London. This group was to became the Royal Society, so Wallis is a founder member of the Royal Society and one of its first Fellows.
Wallis contributed substantially to the origins of calculus and was the most influential English mathematician before Newton. He studied the works of Kepler, Cavalieri, Roberval, Torricelli and Descartes. Then Wallis introduced ideas of the calculus going beyond that of these authors.
In Arithmetica infinitorum (1656) Wallis evaluated the integral of (1-x2)n from 0 to 1 for integral values of n, building on Cavalieri's method of indivisibles. He devised a method of interpolation in an attempt to compute the integral of (1-x2)1/2 from 0 to 1. Using Kepler's concept of continuity he discovered methods to evaluate integrals which were later used by Newton in his work on the binomial theorem. Newton says
About the beginning of my mathematical studies, as soon as the works of our celebrated countryman, Dr Wallis, fell into my hands, by considering the Series, by the Intercalation of which, he exhibits the Area of the Circle and the Hyperbola....
In Arithmetica infinitorum Wallis also established the formula
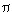 /2 = (2.2.4.4.6.6.8.8.10..)/(1.3.3.5.5.7.7.9.9...)
/2 = (2.2.4.4.6.6.8.8.10..)/(1.3.3.5.5.7.7.9.9...)
In his Tract on Conic Sections (1656) Wallis described the curves that are obtained as cross sections by cutting a cone with a plane as properties of algebraic coordinates without the embranglings of the cone. He followed methods in the style of Descartes' analytical treatment.
Wallis was also an important early historian of mathematics and in his Treatise on Algebra he has a wealth of historical material. However the most important feature of this work, which appeared in 1685, is that it brought to mathematicians the work of Harriot in a clear exposition.
In Treatise on Algebra Wallis accepts negative roots and complex roots. He shows that a3 - 7a = 6 has exactly three roots and that they are all real. He also criticises Descartes' Rule of Signs stating, quite correctly, that the rule which determines the number of positive and the number of negative roots by inspection, is only valid if all the roots of the equation are real.
Wallis introduced our present symbol  for infinity.
for infinity.
He also restored some ancient Greek texts such as Ptolemy's Harmonics, Aristarchus's On the magnitudes and distances of the sun and moon and Archimedes' Sand-reckoner.
His non-mathematical works include many religious works, a book on etymology and grammar Grammatica linguae Anglicanae (Oxford, 1653) and a logic book Institutio logicae (Oxford, 1687).
Wallis had a bitter dispute with Hobbes, who although a fine scholar, was far from Wallis's class as a mathematician. In 1655 Hobbes claimed to have discovered a method to calculate the area of a circle by integration. Wallis's book with his methods was in press at the time and he refuted Hobbes's claims. Hobbes replied to the
... insolent, injurious, clownish language
of Wallis with the pamphlet Six lessons to the Professors of Mathematics at the Institute of Sir Henry Savile. Wallis replied with the pamphlet Due Correction for Mr Hobbes, or School Discipline for not saying his Lessons Aright to which Hobbes wrote the pamphlet The Marks of the Absurd Geometry, Rural Language etc. of Doctor Wallis. The dispute continued for over 20 years, becoming extended to include Boyle, and ending only with Hobbes's death.
Article by: J J O'Connor and E F Robertson
Click on this link to see a list of the Glossary entries for this page

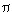 /2 = (2.2.4.4.6.6.8.8.10..)/(1.3.3.5.5.7.7.9.9...)
/2 = (2.2.4.4.6.6.8.8.10..)/(1.3.3.5.5.7.7.9.9...)
 for infinity.
for infinity.